Outline of Course
As stated earlier, our aim to estimate lift in the first part of this course.
Since viscosity contributes little towards the lift force, we have decided to work with the invscid flow equations.
Further more, as we are only interested in the low speed regime of flight, the flow is incompressible.
\[ \frac{D \rho}{D t} = 0 \]
Therefore, the mass conservation equation simplifies to: \[ \nabla \cdot \mathbf{U} = 0 \]
Physical meaning of a divergence free field
The divergence of a vector field at a point is a measure of the net flow of the field out of an infinitesimal volume surrounding that point. If the vector field is velocity, then it
If the divergence of a field is zero, it means that the field is incompressible.
Read section 2.12 from Anderson (2011) for more details. Especially the paragraph after equation 2.126c towards the end of the section.
Similarly, we can show that the momentum equation translates into the Bernoulli’s equation for incompressible flow.
\[ p + \frac{1}{2} \rho | \mathbf{U} |^2 = \text{constant} \]
for a streamline. If the existence of free stream is assumed, then the constant is \(p_{\infty} + \frac{1}{2} \rho_{\infty} | \mathbf{U}_{\infty} |^2\).
So now, if we are only able to solve the mass conservation equation for the velocity field \(\mathbf{U}\), we can find the pressure field \(p\) and hence the lift force.
This is the first approach. Usually, we would find the velocity field by solving the potential flow equation.
However, a much simpler approach is to use the Kutta-Joukowski theorem. This theorem relates the lift force to the circulation around the airfoil.
\[ L = \rho \Gamma U_{\infty} \]
where \(\Gamma\) is the circulation around the airfoil. Clearly, the lift force is proportional to the circulation. So for a given velocity field, the lift force can be maximized by maximizing the circulation. Now that we know the importance of circulation, let us spend some time to get a deeper understanding of circulation.
Circulation
Circulation is a measure of the rotation of the flow around a closed curve. It is a scalar quantity and is defined as the line integral of the velocity field around the curve.
\[ \Gamma = \oint \mathbf{U} \cdot \operatorname{d}\mathbf{l} \]
If we consider the contribution of a small segment of the curve, the circulation is the product of the velocity component tangential to the curve locally and the length of the segment.
If I consider a circular path around a source (\(\phi = \frac{Q}{2\pi r}\)), we can clearly see that the velocity is orthogonal to the path everywhere. Hence, the circulation is zero.
Next, consider a rectangular path in a 2D freestream. The contribution of the edges of the rectangle that are parallel to the free stream, cancels out each other. The contribution of the edges perpendicular to the free stream direction is zero has the velocity is orthogonal to the path everywhere. Hence, the circulation is zero. This argument can be extended to 3D free stream as well.
In fact, consider a general path in a 3D freestream where velocity is \(U_{\infty} \hat{\mathbf{i}}\). The circulation can be calculated as:
\[ \Gamma = \oint U_{\infty} \mathbf{i} \cdot \operatorname{d}\mathbf{l} = U_{\infty} \oint \mathbf{i} \cdot \operatorname{d}\mathbf{l} = U_{\infty} \oint \operatorname{d}x = 0 \]
Hence, the circulation about any closed path in a freestream is zero.
A singly connected domain is a domain where any closed curve can be shrunk to a point without leaving the domain. A doubly connected domain is a domain where there exists a closed curve that cannot be shrunk to a point without leaving the domain.
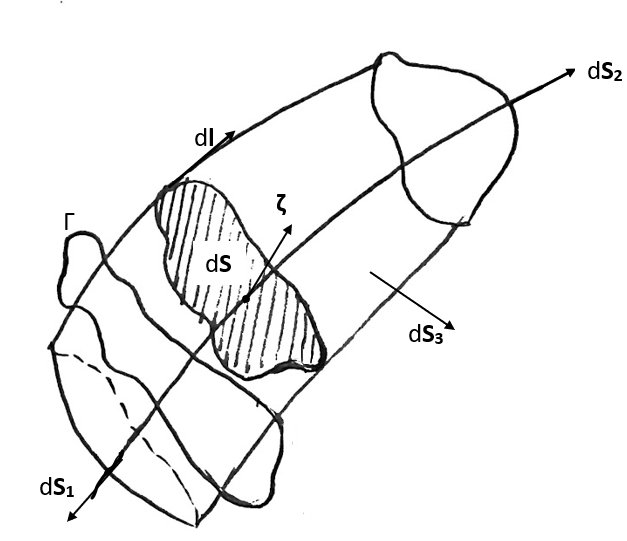
Now let us consider a singly connected domain and apply Stokes theorem to the circulation integral. The circulation integral can be written as:
\[ \Gamma = \oint \mathbf{U} \cdot \operatorname{d}\mathbf{l} = {\subset\!\supset} \llap{\iint}_{\mathbf{S}} \nabla \times \mathbf{U} \cdot \operatorname{d}\mathbf{S} \]
where \(\operatorname{d}\mathbf{S}\) is the surface element of the domain.
This shows that the circulation is intimately related to the curl of the velocity field. Curl of velocity is called vorticity. For the physical interpretation of vorticity, refer to section 2.12 from Anderson (2011).
Vorticity
Vorticity is a measure of the local rotation of the flow. It is a vector quantity and is defined as the curl of the velocity field.
\[ \boldsymbol{\xi} = \nabla \times \mathbf{U} \]
The vorticity vector is orthogonal to the plane of rotation and its magnitude is twice the local rotation rate.
Angular velocity is defined as half the vorticity vector.
\[ \boldsymbol{\omega} = \frac{1}{2} \boldsymbol{\xi} \]
Now, we have seen that the divergence of the velocity field is zero from the mass conservation equation for an incompressible flow. Divergence free vector fields are called solenoidal fields. The curl of a solenoidal field is zero. Hence, the circulation is zero for a solenoidal field.
Here is a proof that shows that if \(\nabla \cdot \mathbf{U} = 0\) then \(\curl \times \mathbf{U} = 0\). The curl of a solenoidal field in zero.
Since the flow is incompressible, the curl of the velocity field is zero. Hence, the circulation is zero.
Read section 2.13 from Anderson (2011) for more details.