Assignment 1
The aim of this assignment is to refresh various derivations and concepts from the course on “Fluid Mechanics”.
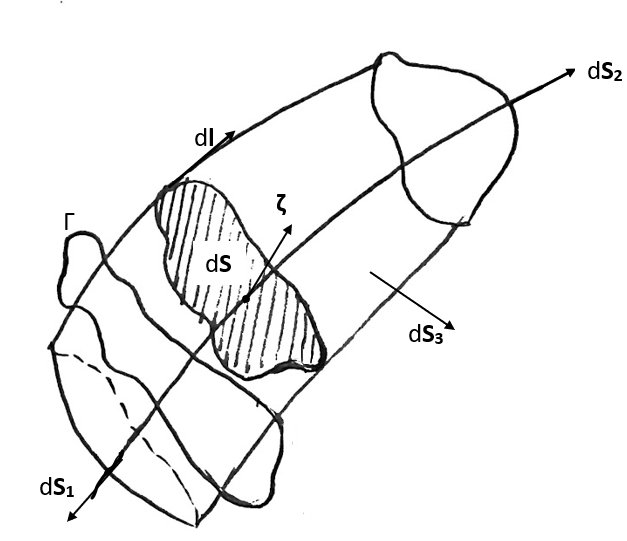
Derive the integral form of mass conservation, energy conservation and momentum conservation equations for a fluid flow. The given equations should be for a general three-dimensional unstead, viscous, compressible flow with no heat addition. You should derive the Lagrangian integral form of the equations. THen discuss the significance of each term in the equations. Then convert the equation to the Eulerian integral form.
Derive the differential form from the above equations.
Convert the above equations to the special case of inviscid flow.
Write the differential equations in the total derivative form. Here, assume the definition of the total derivative but clearly show all other steps for the derivation.
Now, convert the above equations to the special case of incompressible flow.
Deliverables
Hand written derivation.
Deadline
By 20/09/2024 2:00PM in my office.