Irrotational Flow

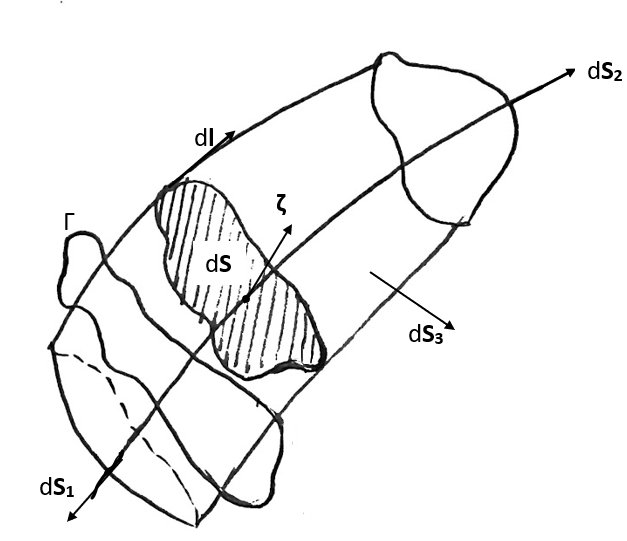
We will explore the concepts of irrotational flow and circulation in this page. Irrotational flow is defined as a flow with zero vorticity everywhere, i.e. \(\nabla \times \vec{U} = 0\). Circulation is simply the integral \(\Gamma = \oint \limits_C \vec{U}\cdot d\vec{l}\) about any closed curve (loop) \(C\).

Then clearly for a simply connected domain, all the closed curves are such that Stokes’s theorem can be applied.

\[\begin{aligned} \Gamma &= \oint \vec{U}\cdot\vec{dl} \\ &= {\subset\!\supset} \llap{\iint}(\nabla\times\vec{U})\cdot\vec{dS} = 0\\ \end{aligned}\]

As per Stokes’s theorem,

\[ \oint\limits_C \vec{U}\cdot\vec{dl} = {\subset\!\supset} \llap{\iint}(\nabla \times \vec{U})\cdot\vec{dS}\]

where \(S\) is any surface enclosed by the closed curve C and there are infinite surfaces of this nature. Now in the domain \(\nabla \times \vec{U} = 0\) and for the boundary \(\Gamma = 0\). But consider a 3D wing and a curve around that wing, that curve can be translated away from the wing such that it encloses only fluid and we can apply Stokes’s theorem. These kinds of domains are called simply connected domains.

But,

\[\begin{aligned} \Gamma &= \oint\limit_C \vec{U}\cdot\vec{dl}\\ &= \oint \nabla \phi\cdot\vec{dl}\\ &= \oint\limits_C d\phi \end{aligned}\]

where, \(\nabla \phi\) is the velocity potential. Now for \(\oint\limits_C d\phi\) to be zero, \(\phi\) has to be a single valued function. A function for which exactly one point in the range corresponds to each point in the domain is single valued function. For a doubly connected region, consider an irrotational flow,

\[\begin{aligned} \Gamma &= \oint\limits_C \vec{U}\cdot\vec{dl}\\ &= \oint\limits_C \nabla\phi \cdot \vec{dl}\\ &= \oint\limits_C d\phi = 0\\ \end{aligned}\]

Consider two closed surfaces naming \(C_1\) and \(C_2\), where \(C_1\) is the curve enclosing the airfoil and \(C_2\) is the curve enclosing both the airfoil and an open fluid element around the airfoil ADCBA. Now taking curve \(C_2\),

\[\begin{aligned} \oint\limits_{C_{2}} \vec{U}\cdot\vec{dl} &= \int_{D}^C + \int_{C}^B + \int_{B}^A + \int_{A}^D\\ \therefore {\subset\!\supset} \llap{\iint}\limits_S (\nabla\times\vec{U})\cdot\vec{dS} &= \int_{D}^C + \int_{C}^B + \int_{B}^A + \int_{A}^D\\ \end{aligned}\]

Assuming A\(\xrightarrow{}\) B and D \(\xrightarrow{}\) C,

\[\begin{aligned} 0 &= \int_{D}^C + \int_{C}^B + \int_{B}^A + \int_{A}^D\\ &= \int_{D}^C - \int_{A}^B + \int_{C}^B - \int_{C}^B\\ \end{aligned}\]

The circulation is constant along all irreducible curves in an irrotational flow.

Now the Stokes’s theorem cannot be applied to curve \(C_1\) and airfoil comes in between \(\nabla\times\vec{U}\) is not defined inside the airfoil. Note that \(\phi\) is no more a single valued function.

\[\phi_{B}^+ - \phi_{B}^- = \Gamma\]

UNIQUENESS OF SOLUTION

1. Simply connected domain

Any domain where any closed curve can be reduced to a point without ever leaving the domain and all 3D domains with finite bodies.

\[\begin{aligned} \nabla^2 \phi &= 0\\ \nabla\phi\cdot\hat{n_\infty} &= 0\\ \nabla \phi|_\infty &= \vec{U}_\infty\\ \end{aligned}\]

PROOF:

Let \(\phi_1\) and \(\phi_2\) be two solutions that satisfy this equation. Then,

\[\begin{aligned} \psi &= \phi_1 - \phi_2\\ \nabla^2 \psi &= \nabla^2 \phi_1 - \nabla^2 \phi_2 =0\\ \end{aligned}\]

\[\nabla\psi\cdot\hat{n_\infty} = \nabla\phi_1\cdot\hat{n_\infty} - \nabla\phi_2\cdot\hat{n_\infty} = 0-0 =0\]

\[ \nabla\psi|_\infty = \nabla\phi_1|_\infty-\nabla \phi_2|_\infty = \vec{U_\infty} - \vec{U_\infty} =0\]

Now by divergence theorem,

\[{\subset\!\supset} \llap{\iint}\limits_S \psi \nabla \psi\cdot \vec{dS} = {\large{\subset\!\supset}} \llap{\iiint}_\forall \nabla\cdot(\psi\nabla\psi) d\forall\\\]

From equation 1,

\[\begin{aligned} {\large{\subset\!\supset}} \llap{\iiint}_ \forall \nabla\cdot(\psi\nabla\psi)d\forall &= {\large{\subset\!\supset}} \llap{\iiint}_\forall \tiangledown \psi \cdot \nabla \psi d\forall + {\large{\subset\!\supset}} \llap{\iiint}\psi \nabla^2 \psi d\forall\\ |\nabla\psi|^2 &= \nabla \psi \cdot \nabla \psi \\ \nabla^2\psi &= 0\\ \end{aligned}\]

From equation 1 and 2,

\[\begin{aligned} {\large{\subset\!\supset}} \llap{\iiint}_\forall |\nabla\psi|^2 d\forall &= {\subset\!\supset} \llap{\iint}_S \psi \nabla\psi \vec{dS} + {\subset\!\supset} \llap{\iint}_S \psi \nabla\psi\cdot\vec{dS}\\ {\large{\subset\!\supset}} \llap{\iiint}_\forall |\nabla\psi|^2 d\forall &= 0\\ \end{aligned}\]

Since,

\[|\nabla\psi|^2 \ge 0\]

Therefore, everywhere

\[\begin{aligned} \nabla\psi = 0 \\ \nabla (\phi_1-\phi_2) &= 0\\ \therefore \phi_1 &= \phi_2 + C\\ \end{aligned}\]

Hence, the velocity potential is defined to be a constant for a simply connected domain.

A flow is irrotational if it is - barotropic, - inviscid, and - there exist a freestream i.e flow should have some region where there is uniform flow (Zero circulation, \(\Gamma = 0\)).

We know that for irrotationality,

\[\begin{aligned} \nabla\times\vec{U} &= 0 \end{aligned}\]

\(\vec{U}\) is the flow velocity vector and \(\nabla\) is the divergence.

Curl operator in the