Reynolds’s Transport Theorem
- In calculus it is known as the Liebnitz theorem.
We will prove this theorem for mass conservation. The simplest statement of conservation of mass is m = constant. However, this is of little use.
Instead we consider \(\frac{dm}{dt}=0\)
\[\begin{aligned}
\frac{d}{dt} \oiiint_{{\ooalign{\hfil$V$\hfil\cr\kern 0.08em--\hfil\cr}}(t)} \rho(\vec{r},t) d{\ooalign{\hfil$V$\hfil\cr\kern 0.08em--\hfil\cr}}&= 0 \\
\frac{d\alpha}{dt} &= 0 \\\end{aligned}\] where, \(\alpha = \oiiint_{{\ooalign{\hfil\)V\(\hfil\cr\kern 0.08em--\hfil\cr}}(t)} \rho(\vec{r},t) d{\ooalign{\hfil\)V\(\hfil\cr\kern 0.08em--\hfil\cr}}\). \[\begin{aligned}
\lim_{\Delta t\to 0} \frac{\alpha(t+\Delta t) - \alpha (t)}{\Delta t} &= 0 \\\end{aligned}\] Now, \[\begin{aligned}
\alpha (t) &= \oiiint_{\tikz[baseline=(char.base)]{
\node[shape=circle,draw,inner sep=2pt] (char) {1};}} \rho(\vec{r},t) d{\ooalign{\hfil$V$\hfil\cr\kern 0.08em--\hfil\cr}}+ \oiiint_{\tikz[baseline=(char.base)]{
\node[shape=circle,draw,inner sep=2pt] (char) {2};}} \rho(\vec{r},t) d{\ooalign{\hfil$V$\hfil\cr\kern 0.08em--\hfil\cr}}\hspace{25mm} \tikz[baseline=(char.base)]{
\node[shape=circle,draw,inner sep=2pt] (char) {A};} \\
\alpha (t+\Delta t) &= \oiiint_{\tikz[baseline=(char.base)]{
\node[shape=circle,draw,inner sep=2pt] (char) {2};}} \rho(\vec{r},t+\Delta t) d{\ooalign{\hfil$V$\hfil\cr\kern 0.08em--\hfil\cr}}+ \oiiint_{\tikz[baseline=(char.base)]{
\node[shape=circle,draw,inner sep=2pt] (char) {3};}} \rho(\vec{r},t+\Delta t) d{\ooalign{\hfil$V$\hfil\cr\kern 0.08em--\hfil\cr}}\hspace{10mm} \tikz[baseline=(char.base)]{
\node[shape=circle,draw,inner sep=2pt] (char) {B};} \\\end{aligned}\] We note here that we have quantities here at \(t+\Delta t\) and also in region . We wish to convert all of them to time t and region and .
Consider point O in region . It can be extrapolated around point B using Taylor series. Therefore, \[\begin{aligned}
\left.\rho (\vec{r},t+\Delta t)\right|_O &= \left.\rho(\vec{r},t)\right|_B + \left.\frac{\partial {\rho (\vec{r},t)}}{\partial t}\right|_B \Delta t + \nabla \rho (\vec{r},t) . \Delta\vec{r} + HOT \hspace{10mm} \tikz[baseline=(char.base)]{
\node[shape=circle,draw,inner sep=2pt] (char) {C};}\end{aligned}\] where, HOT = higher order terms.
Similarly, for , \[\begin{aligned}
\left.\rho(\vec{r},t+\Delta t)\right|_{\tikz[baseline=(char.base)]{
\node[shape=circle,draw,inner sep=2pt] (char) {2};}} &= \left.\rho(\vec{r},t)\right|_{\tikz[baseline=(char.base)]{
\node[shape=circle,draw,inner sep=2pt] (char) {2};}} + \left.\frac{\partial\rho}{\partial t}\right|_{\tikz[baseline=(char.base)]{
\node[shape=circle,draw,inner sep=2pt] (char) {2};},t} \Delta t + HOT
\hspace{25mm} \tikz[baseline=(char.base)]{
\node[shape=circle,draw,inner sep=2pt] (char) {D};}\end{aligned}\]
Therefore, \[\begin{aligned}
\frac{d}{dt} \oiiint_{{\ooalign{\hfil$V$\hfil\cr\kern 0.08em--\hfil\cr}}(t)} \rho(\vec{r},t) d{\ooalign{\hfil$V$\hfil\cr\kern 0.08em--\hfil\cr}}&= \lim_{\Delta t\to 0} \frac{\alpha(t+\Delta t) - \alpha (t)}{\Delta t} \\
&= \lim_{\Delta t\to 0} \frac{1}{\Delta t} \{ \oiiint_{\tikz[baseline=(char.base)]{
\node[shape=circle,draw,inner sep=2pt] (char) {3};}} \rho(\vec{r},t+\Delta t) d{\ooalign{\hfil$V$\hfil\cr\kern 0.08em--\hfil\cr}}- \oiiint_{\tikz[baseline=(char.base)]{
\node[shape=circle,draw,inner sep=2pt] (char) {1};}} \rho(\vec{r},t) d{\ooalign{\hfil$V$\hfil\cr\kern 0.08em--\hfil\cr}}+ \oiiint_{\tikz[baseline=(char.base)]{
\node[shape=circle,draw,inner sep=2pt] (char) {2};}} [\rho(\vec{r},t+\Delta t) - \rho(\vec{r},t)] d{\ooalign{\hfil$V$\hfil\cr\kern 0.08em--\hfil\cr}}\}\end{aligned}\] Now, we note that \[\begin{aligned}
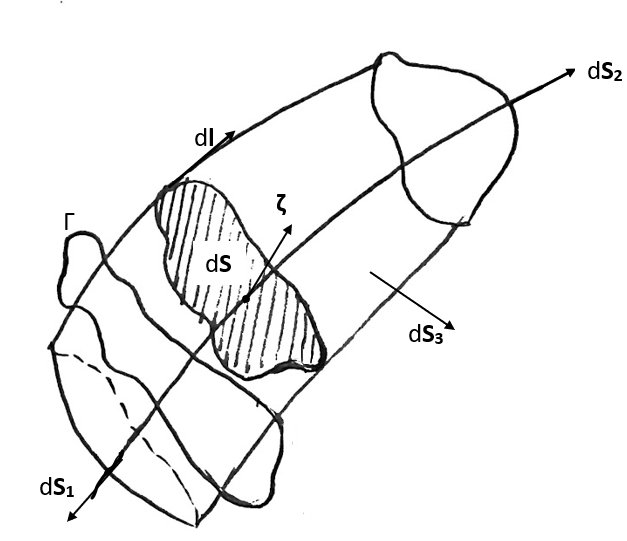
d{\ooalign{\hfil$V$\hfil\cr\kern 0.08em--\hfil\cr}}&= (\Delta t \vec{u}).\vec{ds} \\
&= \vec{u}.\hat{n} \lvert\vec{ds}\rvert.\Delta t\end{aligned}\] where \(\hat{n}\) is the unit normal to the surface. Since we are demanding that a C.V. has to be closed, \(\hat{n}\) is outward pointing by definition. [Note: Inward/Outward cannot be determined if we do not have a closed volume.]
Also, we use and to obtain. \[\begin{aligned}
RHS &= \lim_{\Delta t\to 0} \frac{1}{\Delta t} [ \oiint_{P-B-Q} (\rho(\vec{r},t) + \frac{\partial\rho}{\partial t} \Delta t + \nabla\rho.\Delta\vec{r}) \vec{u}.\vec{ds} \Delta t +
\oiint_{Q-C-P} (\rho(\vec{r},t) + \nabla\rho.\Delta\vec{r}) \vec{u}.\vec{ds} \Delta t + \oiiint_{\tikz[baseline=(char.base)]{
\node[shape=circle,draw,inner sep=2pt] (char) {2};}} \frac{\partial\rho}{\partial t} \Delta t.d{\ooalign{\hfil$V$\hfil\cr\kern 0.08em--\hfil\cr}}]\end{aligned}\] Negative sign from \(\vec{ds}\) has been gobbled up inside the dot product. \[\begin{aligned}
RHS &= \oiint_{s} \rho(\vec{r},t) \vec{u}.\vec{ds} + \oiiint_{{\ooalign{\hfil$V$\hfil\cr\kern 0.08em--\hfil\cr}}} \frac{\partial\rho}{\partial t} d{\ooalign{\hfil$V$\hfil\cr\kern 0.08em--\hfil\cr}}\end{aligned}\] As \(\Delta t\) goes to zero, \(\tikz[baseline=(char.base)]{ \node[shape=circle,draw,inner sep=2pt] (char) {2};}\) goes to \({\ooalign{\hfil\)V\(\hfil\cr\kern 0.08em--\hfil\cr}}(t)\)
Therefore,
The above equation is the equation of Reynold’s Transport Theorem. The LHS is the Lagrangian term and is dependent on time, while the RHS is the Eulerian term and is independent of time.
The first term on RHS denotes the change due to the unsteady changes in density. This term is zero for steady flows when \(\frac{\partial\rho}{\partial t} =0\).
The second term on RHS denotes the net inflow/outflow of the quantity out of the C.V. That is the flux of the quantity \(\rho.\vec{u}\).
Note here that \(\vec{u}\) has been used for two things. Velocity of the boundary of C.V. and velocity of flow. But since the Lagrangian C.V. boundary moves with the same speed as the fluid, they are one and the same.
Now this theorem is a general theorem for any transported quantity i.e., mass, momentum, energy. Pressure is not a transport quantity.